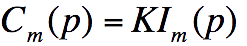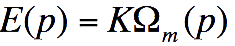TP REPONSE FREQUENTIELLE DES SYSTEMES ASSERVIS
Étude
de la cheville NAO - Activités des
modélisateurs

La cheville est constituée du pied, de la cheville et du tibia.
Le mouvement est assuré par un moteur à courant continu.



Pied Cheville
Tibia

La structure globale de l'asservissement est représentée ci-dessous :

L'objectif de votre partie est de compléter un modèle causal de la
partie "conversion d'énergie" (le moteur à courant courant continu) et de
l’asservissement avec correction proportionnelle.
En revanche, la partie "transmission de l'énergie" sera modélisée de
façon acausale, les éléments de ce modèle étant issus d'une maquette
numérique.
Construction du modèle
Le modèle ébauché est disponible
au téléchargement
Ouvrir Matlab, et ouvrez le fichier "cheville_light.slx".
Faites apparaître l'explorateur de bibliothèque (l'équivalent Matlab
des palettes sous Scilab).

Le modèle ci-dessous correspond à la forme du modèle complet auquel
vous devez aboutir (ATTENTION : dans cette image, toutes
les fonctions qui apparaissent n'ont pas les bonnes valeurs :
ce sera à vous de les renseigner !)
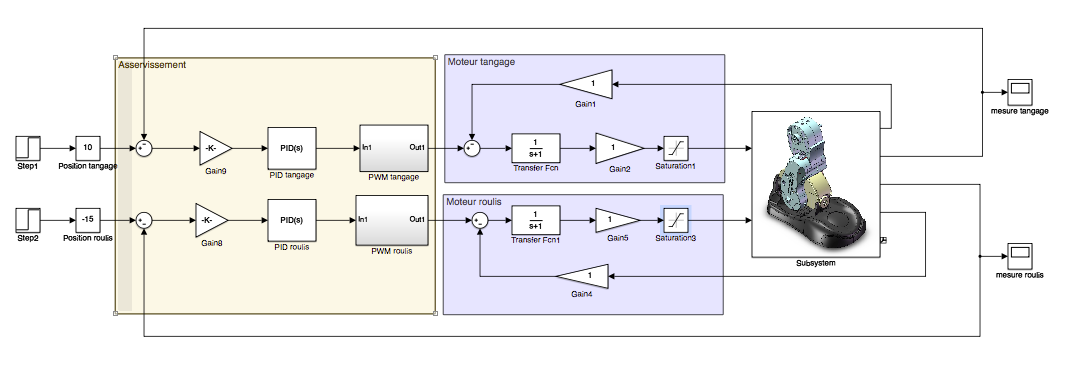
Ce modèle contient la zone relative aux asservissements, aux deux
zones correspondant aux moteurs, et à une zone relative à la modélisation
acausale du mécanisme. Elles sont toutes complétées, à l'exception de
celles des moteurs qu'il vous faudra construire.
Construction du modèle causal des
moteurs
Les modèles de connaissance des deux
moteurs identiques vous sont fournies, exprimées dans le domaine
symbolique :

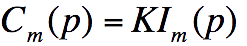
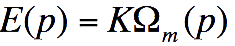
Par ailleurs, il faut installer une limitation du courant. Cette
limitation se modélise par un objet "saturation" dans la bibliothèque
"Simulink > Discontinuités".
Compléter l'ensemble des blocs du modèle à l'aide des
équations du modèle de connaissance et de la documentation technique.
Configuration des correcteurs
Afin de comparer les résultats de chacun,
il est indispensable que les paramètres de fonctionnement soient les
mêmes pour chaque équipe. Il a été décidé de fixer un échelon en tangage
de 30°, avec une correction proportionnelle Kp=500
Simulation

Remarque importante : il est indispensable,
pour que la visualisation de la maquette numérique soit effective, que le
répertoire de travail soit celui dans lequel se trouvent les fichiers .stl
de la simulation.
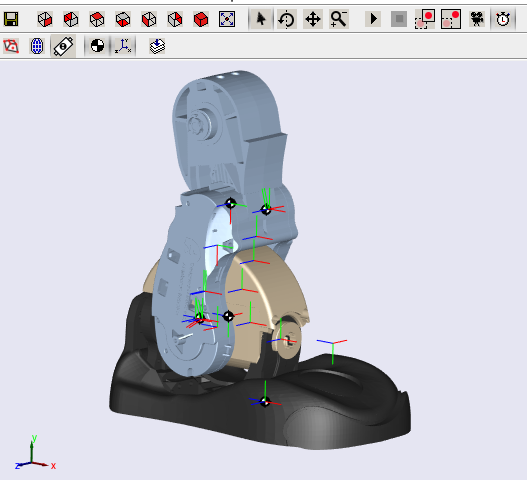
Avant de lancer la simulation, il
faut mettre à jour le diagramme. Cette action vous permettra de
visualiser le comportement de la maquette numérique de la cheville en
même temps que la simulation progresse.
Pour faire cette mise à jour, cliquer sur "Simulation > Mise à
jour" ou taper sur les touches Ctrl+D
La maquette numérique s'affiche alors dans une fenêtre. Il vous est
possible de zoomer et changer d'orientation de vue avec des
manipulations de souris similaires à Solidworks.
Après avoir saisi les consignes dans votre
modèle (30 en tangage et 0 en roulis) et les valeurs du
correcteur PID (Kp=500, Ki=0, Kd=0), lancez la
simulation et observez le comportement de la cheville
dans la fenêtre graphique.
Enregistrement vidéo de la simulation
Il est
possible d'enregistrer au format .avi la simulation, à
des fins de compte-rendu par exemple. Il faut pour cela cliquer sur
l'icône de la caméra, ou cliquer sur le menu "Simulation >
Enregistrer au format AVI"
Conclusion
Comparez
votre résultats avec les autres membres de votre équipe.
Des écarts existent... Recherchez les causes des écarts avec
l'ensemble du groupe
Correction Proportionnelle - Intégrale
Un modèle simplifié, mais qui tient compte des couples résistants,
vous est disponible au
téléchargement . Ce modèle contient un correcteur PI, initialement
réglé avec Kp=100.
Exécuter la simulation, et conclure sur les performances de
l'asservissement en terme de précision et de stabilité.
Expliquer l'existence d'une erreur statique alors que la
boucle ouverte est de classe 1.
Remarque : l'objet "Diagrammes de Bode" permet d'afficher les
diagrammes de gain et de phase de la boucle ouverte.
Réglage de l'action
intégrale
On règle en premier lieu la précision du
système, grâce à une action intégrale. On souhaite ne pas dégrader la
stabilité de plus de 5°.
En déduire la valeur de la pulsation de cassure du
correcteur PI.
En déduire alors la valeur de l'action intégrale Ki.
Modifier
le correcteur PI du modèle Matlab avec cette nouvelle valeur, et
conclure sur la précision, la rapidité et la stabilité du système.
Réglage de l'action
proportionnelle
On choisit de régler ensuite
la rapidité du système. On souhaite que la bande passante du système
s'élève à 30 rad/s.
Calculer la valeur de la correction proportionnelle qui
permet d'obtenir cette banque passante.
La modification de Kp influence la valeur de la pulsation de cassure
du correcteur PI.
Calculer la nouvelle valeur à paramétrer pour l'action
intégrale.
Modifier le correcteur PI du modèle Matlab avec cette
nouvelle valeur, et conclure sur la
précision, la rapidité et la stabilité du
système.
FIN DE CETTE PARTIE
Haut de page