TP REGIMES NON SINUSOÏDAUX
B.2.1 : Étude des tensions composées de l'onduleur - Activités
du chef de projet
Mise en situation et objectifs
Le réseau triphasé est un réseau constitué de trois phases, dont le
potentiel
V de chacune d'elle par rapport au neutre est appelé tension simple.

Les
tensions U entre deux phases sont appelées tensions composées.
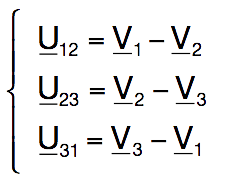
Les courants I transitant dans chacune de ces phases sont appelés
courants de ligne.
Dans un couplage en triangle, les courants circulant dans chacun des
dipôles sont appelés courants de phase. Par ailleurs, la tension
composée Uij
génère
le courant de phase JIJ.
Les phases sont souvent désignées :
* soit par L1, L2, L3 ;
* soit par U, V, W.
Caractéristiques
du malaxeur
Le moteur du malaxeur possède les caractéristiques suivantes,
qui seront importantes pour la construction des diagrammes de
Fresnel :
* les phases de ce moteur sont couplés en triangle,
* chacune de ces phases sera assimilée à une association en
série d"une bobine d'inductance L et d'une résistance R,
* la fréquence de la tension en sortie de variateur est
égale à 5 Hz,
* la valeur efficace de la tension simple est égale à 20V.
L'objectif
de cette partie est de déterminer les déphasages entre un courant de
ligne et les tensions composées, par construction de différents
diagrammes de Fresnel.
Construction
des tensions composées et des courants de phase
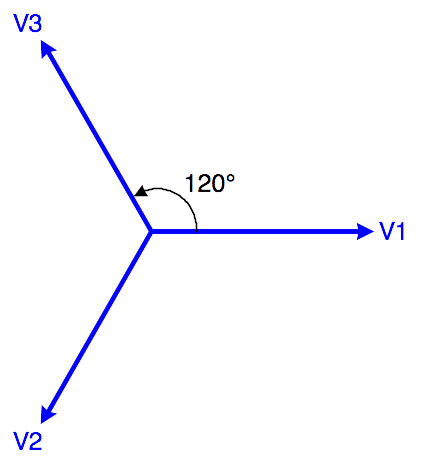 Le réseau triphasé est donc constitué de trois phases,
dont les tensions sont déphasées de 120°.
Le réseau triphasé est donc constitué de trois phases,
dont les tensions sont déphasées de 120°.
La représentation de Fresnel de ces tensions simples est donc la
figure ci-contre.
Question
1
On rappelle que les
tensions composées se déduisent des tensions simples comme suit :
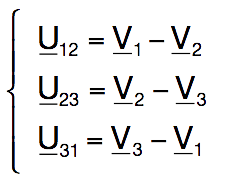
Construire en
rouge le diagramme de Fresnel des tensions composées U12
, U23
, U31
à partir de la représentation en bleu
des tensions simples V1,
V2
et V3.
Il est conseillé d'utiliser les fonctionnalités de dessin d'un logiciel
tel qu'un traitement de texte pour tracer correctement les vecteurs, et
d'utiliser l'échelle suivante : 1 cm <-> 4 V
On rappelle que chaque phase du moteur est modélisée par une bobine
et une résistance en série, avec :
* L=500 mH,
* R=70 Ω.
Vous allez maintenant déterminer le déphasage φJU
du courant de phase par rapport à
la tension composée.
Question
2
 Rappeler
l'expression de l'impédance complexe Z12 de
l'association série d'une bobine et d'une résistance.
Rappeler
l'expression de l'impédance complexe Z12 de
l'association série d'une bobine et d'une résistance.
Etablir l'expression qui
relie la tension complexe U12,
le courant complexe J12,
la résistance R, l'inductance L
et la pulsation ω.
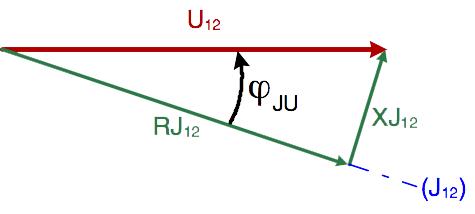
Construire à
l'échelle le diagramme de Fresnel correspondant, et en
déduire la direction du courant J12.
Calculer la valeur du déphasage φJU
du
courant de phase J12,
par rapport à la tension composée U12.
Les trois phases du
moteur sont couplées en triangle. Par conséquent, chacune des phases est
parcourue par un courant de phase composé à partir des courants de
ligne. Vous allez à présent déterminer le déphasage φIJ
du courant de ligne par rapport au courant de phase.
Question
3
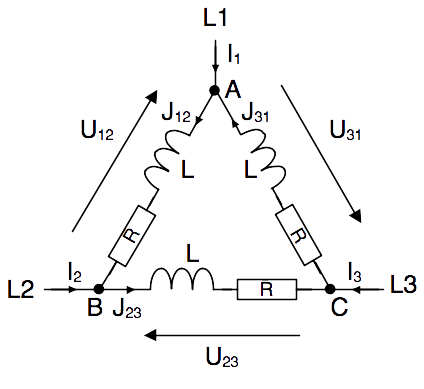
La
figure ci-contre, représentant le couplage en triangle des phases
du moteur, montre la répartition des courant à chacun des nœuds A,
B et C.
Etablir les relations (issues des lois
de Kirchhoff aux noeuds A, B et C) entre les courants de ligne I1,
I2,
I3,
et les courants de phase J12,
J23,
J31.
Construire le
diagramme de Fresnel des courants de phase J12,
J23,
J31
à partir des courants de ligne I1,
I2,
I3.
En déduire enfin à partir du diagramme de
Fresnel le déphasage φIJ
du
courant de ligne I1
par rapport au courant de phase J12.
Question
4
A
partir du déphasage
φIJ
du
courant de ligne I1
par
rapport au courant de phase J12
et du déphasage φJU
du courant de phase J12
par
rapport à la tension composée U12.
calculer la valeur du déphasage φIU
du courant de ligne I1
par
rapport à la tension composée U12.
En déduire les valeurs de ce courant
de ligne I1
par
rapport aux autres tensions composées U23.et
U31.
FIN
DE CETTE PARTIE
Haut
de page
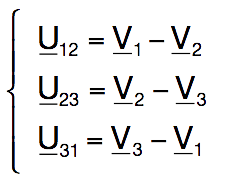

 Le réseau triphasé est donc constitué de trois phases,
dont les tensions sont déphasées de 120°.
Le réseau triphasé est donc constitué de trois phases,
dont les tensions sont déphasées de 120°.

