TP REGIMES NON SINUSOÏDAUX
B.1.1 : Étude du redresseur - Activités du
chef de projet
Mise en situation et objectifs
Un pont redresseur à diodes couplé à un condensateur de lissage de la
tension consomme un courant
qui n'est pas sinusoïdal :

Le courant i(θ) s'exprime sur l'intervalle angulaire α par la relation
suivante, en plaçant l'axe de référence à π/2 rad :

Il
va falloir dans cette partie déterminer certaines caractéristiques de
ce courant, et calculer les harmoniques de courant. Vous chercherez
ensuite à dimensionner un filtre qui permettra de supprimer certains
de ces harmoniques.
B.1.1
Caractéristiques électriques du courant
La tension et le courant en entrée du redresseur sont caractérisés par
:

Question
1
Calculer
la valeur efficace I du
courant i(θ).
On montre que la décomposition en série de Fourier du signal i(θ)
est :
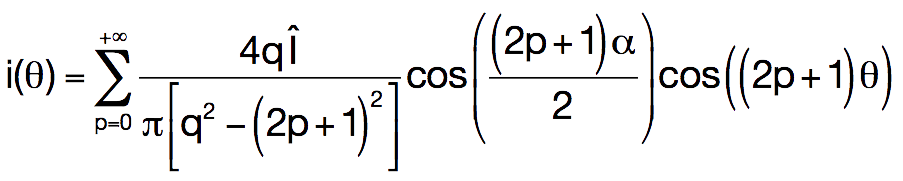
Question
2
Les harmoniques
sont donc tous de rang impair, et ont pour expression :

Compléter le tableau
ci-dessous en calculant les harmoniques h3 et h5 de rangs 3 et 5
:

Tracer sur le spectre
ébauché ci-dessous les raies des fréquences manquantes :

La connaissance de la valeur efficace du fondamental du courant permet
de calculer les puissances transitant dans le
récepteur.
Question
3
Calculer
:
- la puissance active P
- la puissance réactive Q
- la puissance apparente S
En déduire la valeur de la puissance
déformante D liée à la circulation des harmoniques de courant.
Calculer le taux de distorsion harmonique par
rapport au fondamental THD(F)
Question
4
Les
modélisateurs et les expérimentateurs ont respectivement simulé et
mesuré ce spectre.
Comparer votre résultat aux valeurs fournies
par ces deux équipes.
B.1.4
Filtrage des harmoniques
On souhaite supprimer les harmoniques de rang 3 et 5 du courant (on
rappelle que la fréquence du fondamental est égale à 50 Hz). Il faudra
donc installer deux filtres pour dérouter chacun de
ces deux harmoniques.
Question
5
Les filtres
installés pour filtrer ces harmoniques sont des filtres LC. On note
C3 et L3
les caractéristiques du filtre de l'harmonique de rang 3. De même, C3
et L3
sont les caractéristiques du filtre de l'harmonique de rang 5.
On impose L3=1
mH.
Calculer la valeur de la pulsation ω3.
En déduire la valeur de la capacité C3
qui permettrait de filtrer l'harmonique de rang 3.
Pour filtrer l'harmonique de rang 5, on souhaite utiliser un
condensateur de même valeur que C3.
Calculer
la valeur de la pulsation ω5.
En déduire la valeur de la capacité L5
qui permettrait de filtrer l'harmonique de rang 5.
Question
6
Compléter
le schéma
ci-dessous en repassant en dessinant les filtres LC
précédemment dimensionnés, et en indiquant par les couleurs
adéquates les chemins des courants déroutés dans les filtres :

FIN
DE CETTE PARTIE
Haut
de page