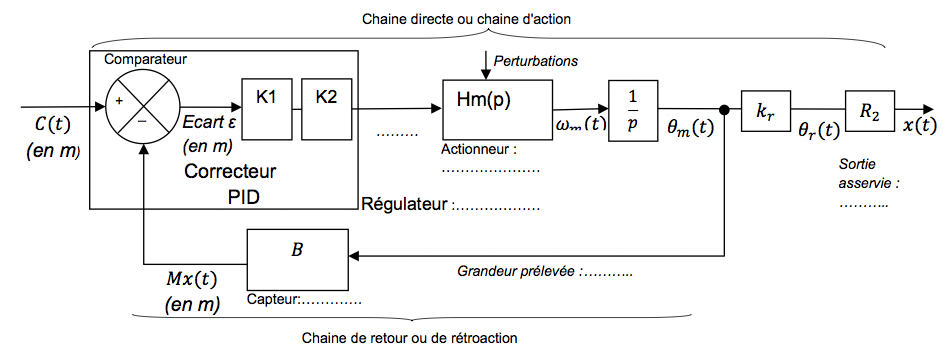
Chaîne de retour
Ecriture du modèle de connaissance
dans le domaine symbolique du moteur
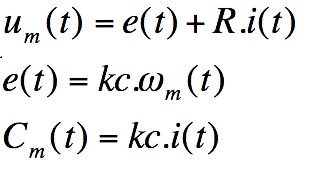

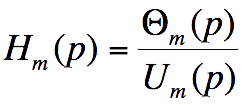
Fonction de transfert en boucle
ouverte
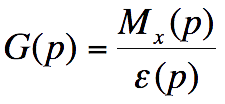
Précision
Rapidité

Stabilité