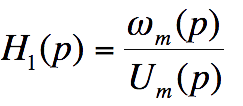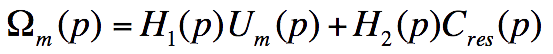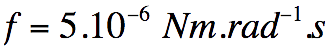TP REPONSE FREQUENTIELLE DES SYSTEMES ASSERVIS
Étude
de la cheville NAO - Activités du chef de
projet

La cheville est constituée du pied, de la cheville et du tibia.
Le mouvement est assuré par un moteur à courant continu.


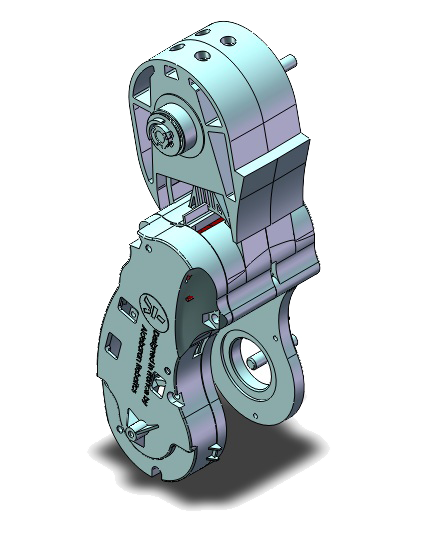
Pied Cheville
Tibia

La détermination du modèle de la cheville débutera par la modélisation
de son moteur.
Puis il faudra insérer ce modèle dans un modèle plus complet qui
prendra en compte les autres éléments composant la cheville.
Le modèle global de l'asservissement est le suivant :

Modélisation du moteur
Les équations du modèle de connaissance du moteur, ainsi que ses
caractéristiques chiffrées, sont fournies dans le document Notices et
performances".
La structure du schéma-bloc du moteur vous est fournie
:
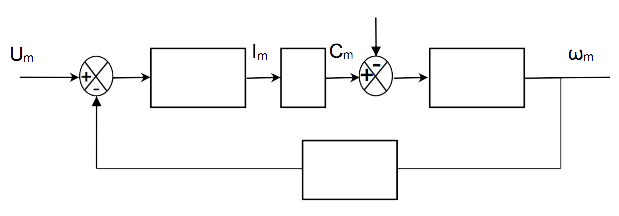
Cette structure à 2 entrées fait intervenir la tension d'alimentation
Um et le couple de frottement sec Csec. Il faudra donc appliquer le
théorème de superposition pour déterminer la réponse ωm(p)
Détermination de la fonction de transfert H1(p)=Um(p)/ωm(p)
A l'aide des équations du modèle de
connaissance du document ressource, compétez le schéma bloc ci-dessus.
En déduire l'expression de la fonction de transfert H1(p), en
supposant le couple résistant nul :
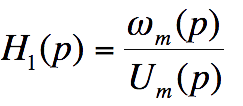
Détermination du temps de réponse
La fonction de transfert H2(p), établie en
supposant la tension
d'alimentation Um nulle, a pour expression :

La fonction de transfert s'écrit alors sous la forme :
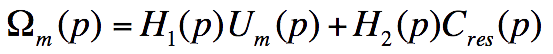
Ecrire la fonction de transfert sous la forme canonique :

Calculer les valeurs de gain, du coefficient d'amortissement et de
pulsation propre, sachant que le coefficient de frottement visqueux est
égal à 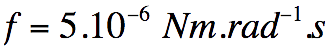
A l'aide des abaques du second
ordre disponibles dans les documents ressource, en déduire la valeur
du temps de réponse du système en boucle ouverte.
Analyse harmonique
A partir de la fonction de transfert établie précédemment, tracez les
diagrammes de Bode asymptotiques. Vous pourrez à cette fin utiliser le
papier semi logarithmique disponible dans les documents ressource.
Modélisation de l'asservissement
Le modèle Matlab de l'ensemble de l'asservissement est ébauché
(disponible en téléchargement)
:

Il reprend l'ensemble de l'asservissement en tangage présenté au début
de cette page : élaboration de la consigne moteur en fonction de l'erreur,
conversion électromécanique, dynamique.
Les fonctions de transfert en rouge sont à compléter par vos soins, en
fonction des résultats obtenus plus haut (cherchez dans l'aide de Matlab.
En cas de doutes, appelez le professeur)
Le correcteur (correction, proportionnelle) est quant à lui identifié
en vert, et devra être renseigné au moment de la simulation.
Mise à jour du modèle
Ouvrez le modèle sous Matlab, et
finalisez-le avec les fonctions de transfert adéquates.
Les modélisateurs et expérimentateurs ont réalisé une série de
tests, dont un avec une correction proportionnelle Kp=500 sur un échelon
en tangage de 30°.
Lancez une simulation avec cette valeur, et observez la réponse
simulée en ouvrant le scope.
Conclusion
Comparez
votre résultats avec les autres membres de votre équipe.
Des écarts existent... Recherchez les causes des écarts avec
l'ensemble du groupe
Diagrammes de Bode par simulation numérique
Matlab permet de mener une analyse harmonique, et d'afficher les
diagrammes de Bode du système.
Il faut d'abord lui indiquer les points correspondant aux entrées et
sorties de la boucle ouverte : clic droit sur la branche adéquate >
Points d'Analyse linéaire > Entrée (ou sortie) de boucle ouverte (On
rappelle que la boucle ouverte est la fonction de transfert entre l'image
de la sortie et l'erreur)
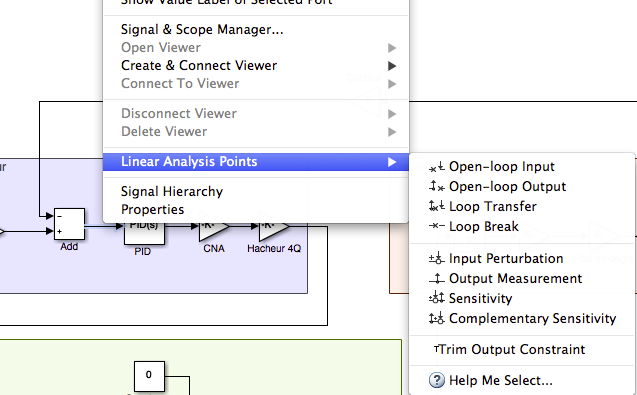
Ceci étant fait, cliquer sur le menu "Analyse > Control Design >
Analyse linéaire"
Sélectionner "Diagramme de Bode"

Conclure sur la stabilité du système
FIN DE CETTE PARTIE
Haut de page