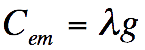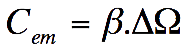TP ALIMENTATION ET CINEMATIQUE DE LA BARRIERE SYMPACT

  Etude de la motorisation de la barrière - Activités du chef de projet
  
     
    Vous allez dans cette partie étudier les caractéristiques du moteur asynchrone présent dans la tête de la barrière. En particulier, vous déterminerez le modèle électrique équivalent de ce moteur.
Etude générale du moteur

    Etude structurelle de la chaîne d'énergie et de l'asservissement

    Le diagramme de bloc interne vous est fourni :

       
    Identifier sur ce diagramme les éléments génériques de tout système pluritechnologique :
        * Alimenter, Distribuer, Convertir, Transmettre pour la chaîne d'énergie
        * Communiquer, Acquérir, Traiter pour la chaîne d'information.

    Au vu de ce diagramme ibd, s'agit-il d'une régulation, d'un asservissement en vitesse, d'un asservissement en position ?

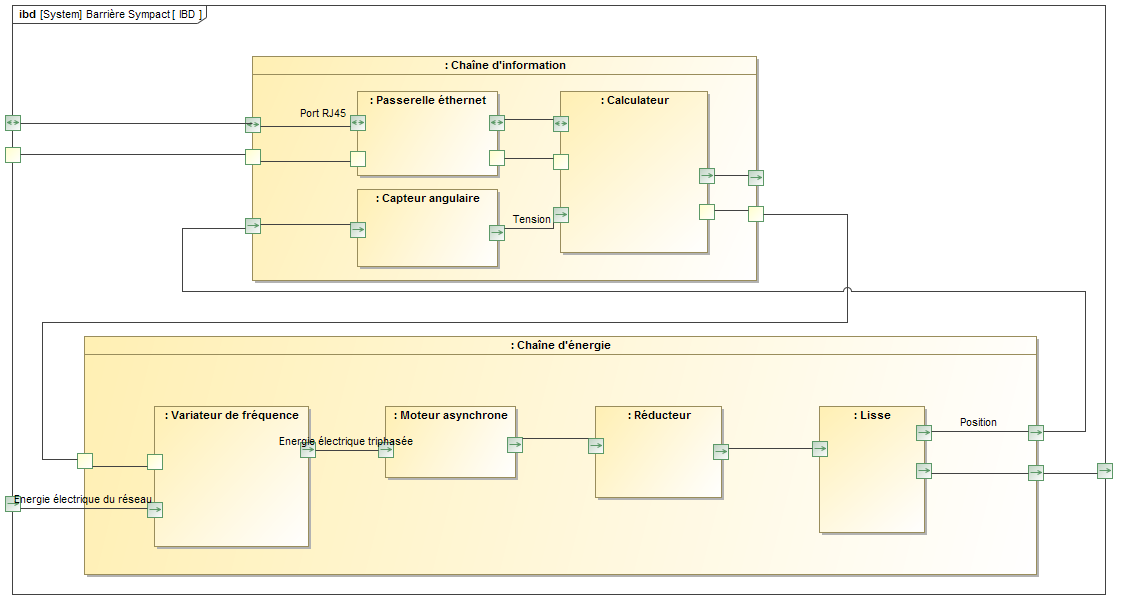
    Alimentation du moteur

    La plaque signalétique du moteur est reproduite ci-dessous :  
       
     On rappelle que la tension simple du réseau d'alimentation est égale à Veff=230V, et que la tension composée est égale à Ueff=400V.
     Sachant que le branchement d'un moteur en étoile est un branchement entre phase et neutre, et que le branchement en triangle est entre deux phases, conclure sur la nature du couplage compatible avec le moteur de la barrière Sympact.
Modélisation électrique du moteur

    Le document suivant résume les notions importantes qui concernent les moteurs asynchrones : Poster_MAS.pdf

    Généralités sur la modélisation du moteur asynchrone

    Le moteur asynchrone est un moteur triphasé, comportant un stator bobiné par phase.
    Lorsque le moteur ne délivre aucun couple, sa vitesse de rotation dépend de la fréquence des signaux du stator. Il s'agit de la vitesse de synchronisme Ns : (avec ω pulsation des signaux, et p  nombre de paires de pôles du stator)
           
    Lorsque le moteur délivre un couple électromagnétique, sa vitesse de rotation diminue. On appelle glissement g la chute relative de vitesse :
           
       
    Sa vitesse de rotation n'est pas fixe, elle dépend du couple électromagnétique. On appelle glissement       
    Chaque phase peut être modélisée de la façon suivante :

          
    V1 : tension efficace sur la bobine du stator
    R1 : résistance de la bobine
    X1 : réactance complexe de fuite du stator
    Rf : résistance fictive modélisant les pertes fer
    Xm : réactance de magnétisation
    X2 : réactance complexe de fuite du rotor
    R2 : résistance d'une phase du rotor
    g : glissement

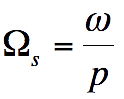
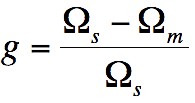
    Détermination de la résistance R1 d'une bobine

   
    On rappelle les schémas des couples étoile ou triangle :
                  
    Moteur isolé, on mesure une résistance entre 2 phases égale à RΩ = 40 Ω. En déduire la valeur de la résistance R1 d'une bobine.

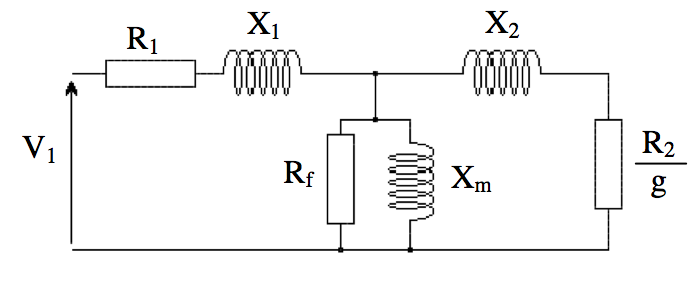
    Détermination des caractéristiques R2 et X2 du rotor

    On effectue à présent un essai rotor bloqué sous tension réduite. On relève alors les puissances et courants suivants :
        * Tension efficace composée : U10=110V
        * Courant efficace de ligne : I10=1,6 A
        * Puissance active consommée : P0=252 W
        * Puissance réactive consommée : Q0=145 VAR

    En négligeant les termes Rf et Xm, en déduire les valeurs de R2 et X2. On rappelle que :
        * rotor bloqué, le glissement vaut g=1
        * la puissance consommée, active ou réactive, est celle consommée par les 3 phases
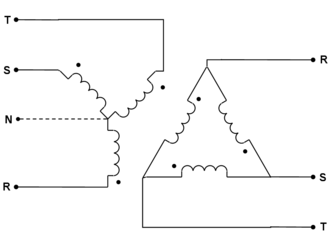
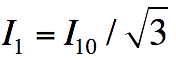        * Le courant efficace dans une phase vaut dans un couplage triangle
Détermination du couple électromagnétique
   

    Expression générale

    Dans cette partie, les grandeurs Rf, Xm et X1 seront négligés.

    Exprimer la puissance électromagnétique Pem en fonction de la vitesse de synchronisme Ns et du couple électromagnétique Cem.

    En déduire l'expression de la puissance électromagnétique en fonction des paramètres V1, R1, R2, X2 et g (On rappelle que la puissance électromagnétique est directement issue de la puissance électrique transitant dans la résistance de phase R2)

    En déduire alors l'expression du couple électromagnétique en fonction de V1, R1, R2, X2, g et Ωs.

    Simplification pour les faibles glissements

    En fonctionnement normal, le glissement est faible et le couple électromagnétique peut être linéarisé :
            
    Exprimer la valeur de ce coefficient λ en fonction de V1, Ωs et R2

    On pose à présent ΔΩ=gΩs. Exprimer la relation entre ΔΩ, Ωs et Ωm

    Pour finir, le couple peut alors être linéarisé en fonction de ΔΩ :
           

    Déterminer l'expression de β en fonction de V1, R2 et Ωs
FIN DE CETTE PARTIE

    Haut de page