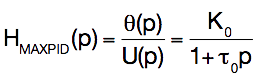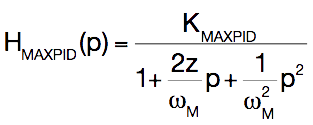TP ASSERVISSEMENT ET CINEMATIQUE DU MAXPID
Modélisation
de l'asservissement - Activités du chef de
projet
Votre objectif est dans un premier temps de modéliser le
comportement du bras Maxpid par sa fonction de transfert et son
schéma-blocs.
Vous aborderez ensuite la notion de correction du comportement en
déterminant le meilleur gain à apporter à l'asservissement.
Identification par réponse indicielle expérimentale
L’identification par réponse indicielle consiste à envoyer une
consigne en échelon au système et d'observer la réponse de ce système. En
fonction de la nature de la réponse, on peut éventuellement conclure sur
l'ordre du système, et conclure quant à ses valeurs caractéristiques
(gain, constante de temps, coefficient d'amortissement, pulsation propre,
...).
Le Maxpid est un système :
* dont la commande est calculée en multipliant l'écart entre la
consigne et la position mesurée par un gain Kp. Ce gain est appelé
"correction à action proportionnelle" ;
* et à retour unitaire.
Identification d'un système du 1er ordre
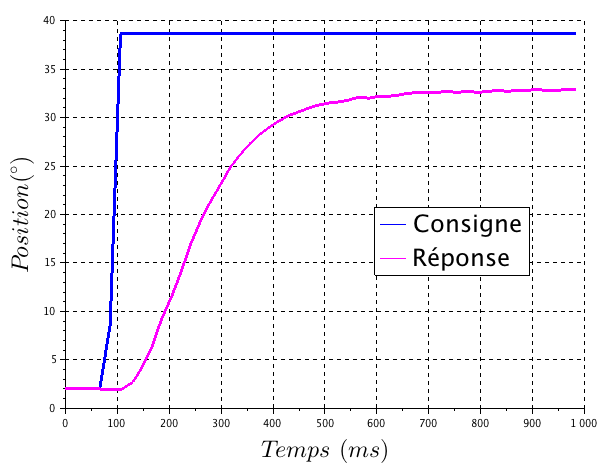
La réponse du Maxpid à une consigne de position pour un gain Kp=20 est
donnée ci-contre.
On cherche dans cette partie à exploiter cette réponse afin
d'identifier la fonction de transfert du Maxpid.
Question
1
Télécharger
le fichier Reponse_Maxpid.scg.
Ce fichier contient les données de la courbe de réponse
indicielle ci-dessus.
Ouvrir Scilab. Dans la
console, taper la commande "figure;" afin
d'ouvrir une fenêtre de figure.
Charger les courbes (Menu de la figure Fichier>Charger...).
Confirmer ou infirmer l’hypothèse d'un système
du 1er ordre, par analyse la forme de la réponse indicielle. Justifier.
Question
2
Par
relevés graphiques, calculer la constante de temps τ
et le gain du système K.
Fonction de transfert en boucle fermée
La courbe que vous venez d'analyser est la réponse du
système asservie, donc en boucle fermée. Par conséquent, le gain
et la constante de temps que vous venez de relever expérimentalement
traduisent à la fonction de transfert en boucle fermée (où θ(p) désigne la
position du bras, et θc(p) la
consigne de position) :
La structure de l'asservissement, à retour unitaire, est donnée
ci-dessous :
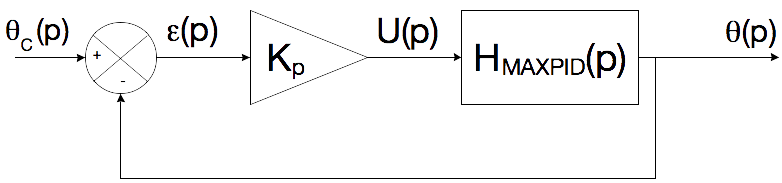
La fonction de transfert du Maxpid seul est une fonction du 1er ordre,
qui s'écrit :
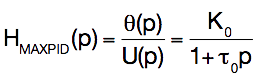
Question
3
Exprimer
la fonction de transfert en boucle ouverte HBO(p)
de cet asservissement.
Exprimer ensuite la fonction de transfert fermée HBF(p)
de cet asservissement.
Question
4
La fonction de transfert en
boucle fermée que vous venez
d'établir correspond à la fonction de transfert
établie à la question 2.
Par identification, en déduire les valeurs de la
constante de temps τ0
et le gain du système K0.
Identification d'un système du 2d ordre
Question
5
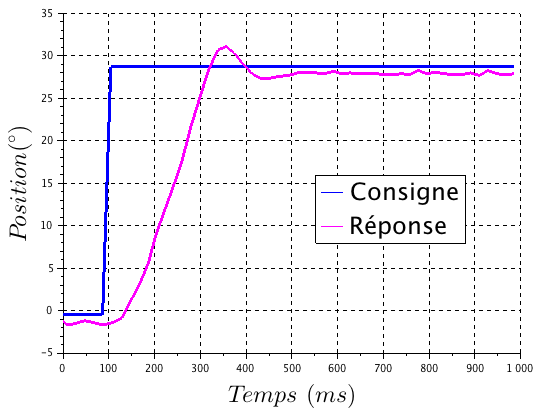A la suite d'un nouvel essai, avec cette fois une
valeur de gain égale à Kp=150, on relève la réponse ci-contre.
Dans Scilab, ouvrir une nouvelle figure et charger
le fichier Reponse_Maxpid2.scg
Le système avec son correcteur peut-il toujours être
identifié comme un système du 1er ordre ? Justifier.
Déterminer le gain de la fonction de transfert en
boucle fermée.
Calculer le 1er dépassement relatif.
Déterminer le temps de montée.
Déterminer la demi-période des
pseudo-oscillations (à prendre entre le 1er pic et le minimum qui suit),
et en déduire la pseudo-pulsation.
Paramètres caractéristiques de la fonction de transfert en
boucle fermée
Question
6
A l'aide des abaques des systèmes du second
ordre, déterminer la valeur du coefficient
d'amortissement m du système en boucle fermé.
A l'aide de la relation entre la peudo-pulsation ωa,
la pulsation
propre ω0 et le
coefficient d'amortissement m, calculer la
valeur de la pulsation propre.
Vérifier cette valeur à l'aide de l'abaque
de la pulsation réduite en fonction du temps de montée.
Question
7
Déduire
des résultats précédents l'expression littérale puis numérique de la
fonction de transfert en boucle fermée sous la forme :
Fonction de transfert en boucle ouverte du système Maxpid
seul
La fonction de transfert du Maxpid est maintenant
supposée être du second ordre, sous la forme :
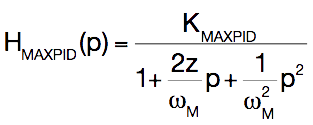
Question
8
Exprimer
la fonction de transfert en boucle ouverte HBO(p)
de cet asservissement.
Exprimer ensuite la fonction de transfert fermée HBF(p)
de cet asservissement.
Par identification avec la fonction de transfert
expérimentale, en déduire les valeurs de la
pulsation propre ωMAXPID,
du coefficient d'amortissement z et du gain du système KMAXPID.
FIN DE CETTE PARTIE
Haut de page