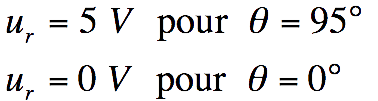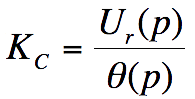TP ASSERVISSEMENT ET CINEMATIQUE DU MAXPID

Modélisation de l'asservissement - Activités des modélisateurs

    L'objectif de cette partie est de vous faire modéliser le système Maxpid sous forme de schéma bloc à a partir du modèle de connaissance.

    Ce schéma fonctionnel sera ensuite traduit sous forme de modèle causal sous Scilab, que vous simulerez.

    Enfin, après avoir demandé aux expérimentateurs une série de mesures, il faudra valider votre modélisation

Structure du Maxpid

    Le système est constitué de différents éléments représentés ci-dessous :

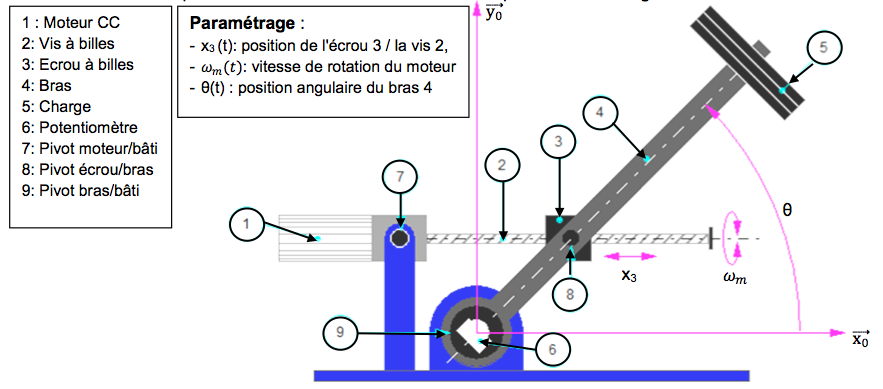
Schéma bloc du Maxpid

    L'ensemble du schéma fonctionnel est complexe, et nécessite de le décomposer en deux parties :
        * une partie "asservissement"
        * une partie "système"

    Nous étudierons en détail dans cette partie la partie "asservissement".

Schéma bloc de l'asservissement

Question 1

Compléter le schéma bloc de l'asservissement ci-dessous, en indiquant en dessous des blocs les composants qui assurent les fonctions :

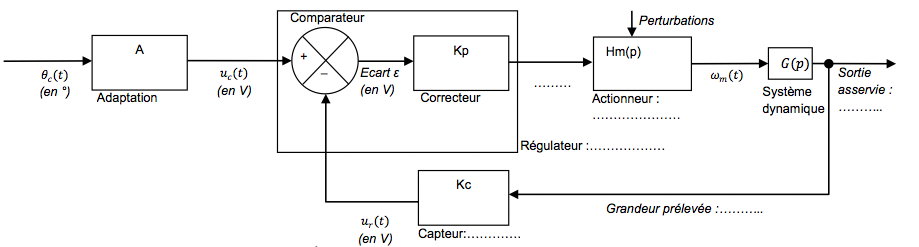
Indiquer, en dessous des traits entre blocs, les grandeurs potentielles manquantes par la lettre usuelle.
Inscrire en rouge au-dessus des traits les grandeurs potentielles dans le domaine de Laplace.

Fonction de transfert de mesure Kc

La chaîne de retour est assurée par un potentiomètre qui délivre une tension ur(t) proportionnelle à l'angle θ(t). Les mesures fournissent :

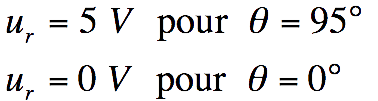
Question 2

    En déduire l'expression du coefficient Kc, et sa valeur numérique en V/°.
    Montrer que dans le domaine symbolique la fonction de transfert s'écrit :

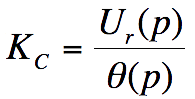
Fonction de transfert d'adaptation A

La consigne est une valeur en °, mais doit être comparée à une tension issue du capteur précédemment étudié. Il faut donc adapter la consigne (en °) en une valeur de tension (en V) de façon à pouvoir mesurer un écart entre consigne et mesure : c'est le rôle de la fonction de transfert d'adaptation A.

Question 3

Donner la relation entre A et Kc pour que l'écart ε soit effectivement l'image de l'écart entre la sortie θ et la consigne θc

Fonction de transfert de la motorisation

Documents ressources pour cette partie:
Modèle de connaissance du bras Maxpid

Les frottements visqueux seront négligés dans l'étude.

Question 3

Prendre connaissance du modèle de connaissance du Maxpid.
Ecrire ces équations dans le domaine symbolique de Laplace.

Question 4

Compléter alors le schéma bloc ci-dessous relatif à la motorisation :

Question 5

En supposant le couple résistant nul, déterminer la fonction de transfert du moteur à écrire sous forme canonique :

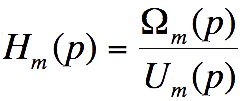
Donner l'ordre et la classe de cette fonction de transfert.

Fonction de transfert du système

Question 6

Déterminer enfin la fonction de transfert du système dynamique sous forme canonique :

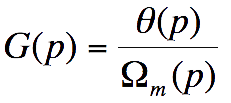
Donner l'ordre et la classe de cette fonction de transfert.

Modélisation causale du Maxpid

Simulation sans perturbation

Question 7

    Ouvrir dans Scilab le fichier Maxpid.zcos.
    Par un clic droit dans la fenêtre graphique du schéma bloc, sélectionner "Modifier le contexte" afin de vérifier que les différentes valeurs correspondent aux valeurs attendues.
    Vérifier par ailleurs que ce schéma bloc correspond bien au schéma bloc que vous avez défini dans la partie précédente.

    Lancer l'étude et observer la réponse temporelle.
    Vérifier qu'elle correspond à la réponse attendue. Justifier votre réponse.

    Ne pas fermer le scope afin de pouvoir comparer cette simulation avec les simulations suivantes.

Question 8

Effectuer l'étude en doublant l'inertie J. En déduire l'impact de la masse sur les performances du système.
Justifier l'impact sur la stabilité.

Influence d'une perturbation

Question 9

    Ouvrir à présent le modèle Maxpid avec poids.zcos. Les paramètres sont les mêmes que ceux de la partie analytique.

    Observer l'impact du poids sur la réponse dans le cas d'un échelon positif ou dans le cas d'un échelon négatif.
    Justifier l'allure l'évolution des réponses.

FIN DE CETTE PARTIE

Haut de page